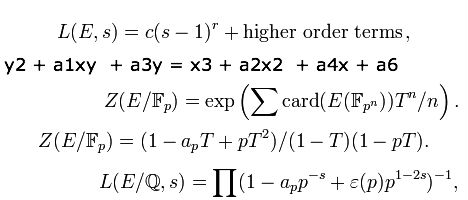Math isn’t just mysterious because the majority of us find it so difficult to understand – it’s also the basis of the universe, giving us clues to physical phenomena like the motion of gases in the atmosphere and the way that physical particles interact with each other amid all the possible variables in three-dimensional space. In math, some of the world’s brightest minds have found bizarre and amazing patterns (and have even turned them into crop circles). Then there are the problems that mathematicians can lose themselves in for years – problems with answers that are so complex, they reach numbers with billions of digits. Solutions to 7 such problems come with a $1 million prize, though it takes years for a judging panel of mathematicians to even determine whether a proposed answer is correct. Care to try your hand?
The Ulam Spiral
Sketching in your notebook when you’re bored in class or at a meeting isn’t always a bad thing – it might just help you discover one of math’s greatest mysteries. That’s exactly what happened when mathematician Stanislaw Ulam doodled on scratch paper during a scientific meeting, writing down rectangular numbers in a spiral with the number 1 at the center. Circling all the prime numbers – numbers that are only divisible by 1 and themselves – Ulam was surprised to note that they formed diagonal lines. Seemingly simple, yet still unexplained, the Ulam spiral is sometimes seen as an example of inherent order in the universe.
The Twin Prime Conjecture
“There are infinitely many primes p such that p + 2 is also prime.” This is the gist of the Twin Prime Conjecture, an open number theory that has never been adequately solved. Twin primes are two prime numbers that differ from each other by only two numbers – 5 and 7, 11 and 13, 29 and 31 and so on. Could you just keep on identifying those twin primes forever and ever? It’s hard to say – both numbers in the largest known twin prime possess an astounding 100,355 decimal digits.
The Collatz Problem
Also known as the 3n + 1 problem, the Collatz Conjecture was posed by L. Collatz in 1937. If you’re not a mathematician and don’t quite get the explanations offered by math sites like Math World, Wikipedia’s version may be simplest: Take any non-negative integer n and if it is even, divide it by 2 to get n/2. If n is odd, multiply it by 3 and add 1 to get 3n + 1. The conjecture is that no matter what numbers you choose, you’ll eventually be left with just 1, no matter how many times you have to repeat the process to get there. A visual demonstration of this problem showing the path for all numbers up to 865 shows an interestingly artistic binary tree.
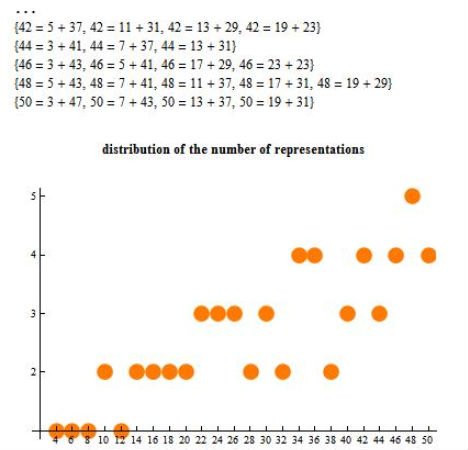
The Goldbach Conjecture
(image via: wolfram demonstrations)
Goldbach’s Conjecture is easy enough to follow: every even number greater than 2 is the sum of two primes – for example, 6 = 3 + 3, 8 = 3 + 5, and so on. But do you have the patience and the understanding of mind bogglingly large numbers to prove that it’s true? A $1 million prize was offered to anyone who could between 2000 and 2002, and it went unclaimed – and still hasn’t been solved.
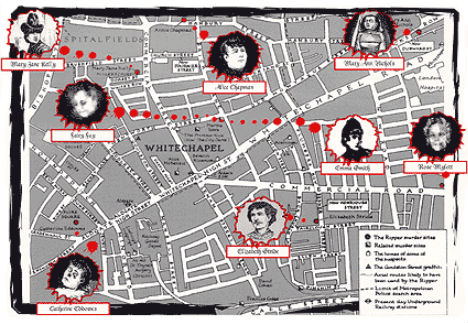
Geospatial Profiling
(image via: london horror tours)
Can math help catch serial killers? Criminal justice professor Kim Rossmo says that a mathematical algorithm that he developed can detect patterns in locations where attacks take place and use that pattern to find the killer’s residence. Called ‘geospatial profiling’, this method has even been employed by the military to find insurgency bases. It’s not exactly unexplained, but still a pretty amazing real-world application of patterns in math. Rossmo has even applied it to the unsolved Jack the Ripper case in London, though the results were impossible to verify.
The Riemann Hypothesis
Some experts say the Riemann Hypothesis is the most important unsolved problem in pure mathematics. The problem deals with the distribution of zeroes in relation to Bernhard Riemann’s ‘Riemann zeta-function’, an analytic number theory that can produce a never-ending sequence of numbers. This formula is so complex that many people (including this typically right-brained writer) fail to grasp it – suffice to say that the world’s brightest mathematicians have been unable to solve it, and that might have something to do with the fact that computer-based calculations have counted at least 100 billion zeroes.
Kepler’s Conjecture
(image via: the paper boy)
What arrangement would produce the densest packing of three-dimensional balls of the same size? This question originated with Sir Walter Raleigh as he mused about the number of cannonballs in a stack, and has led to a problem that still confounds mathematicians. Johannes Kepler, a colleague of Sir Walter’s assistant Thomas Harriot, concluded that the best arrangement is that used by fruit sellers and known as ‘face centered cubic packing’, in which each sphere in the top layer rests within the ‘holes’ of the layer below. No one has been able to improve upon that arrangement or prove that it’s true, but a solution could help physicists understand the structure of crystals.
P Versus NP Problem
Want $1 million in cold hard cash? All you have to do is beat all the mathematicians in the world to solving the P vs. NP Problem. The Clay Mathematics Institute, which is offering the prize, describes it thusly: “Suppose that you are organizing housing accommodations for a group of four hundred university students. Space is limited and only one hundred of the students will receive places in the dormitory. To complicate matters, the Dean has provided you with a list of pairs of incompatible students, and requested that no pair from this list appear in your final choice.” Sound sort of like an SAT question, right? But what you don’t get from reading that paragraph is that the total number of ways in which you could pair up 100 students from that 400 exceeds the number of atoms in the known universe. It would take one hell of a genius computer programmer to solve it.
The Birch and Swinnerton-Dyer Conjecture
(image via: wikipedia)
We’ll have to take the Clay Mathematics Institute’s word for the amazingness of the Birch and Swinnerton-Dyer Conjecture, a numerical investigation of elliptic curves which “asserts that the size of the group of rational (abelian) points is related to the behavior of an associated zeta function near the point s=1”. You have to have a background in complex mathematics to even begin understanding let alone explaining this problem in a way that makes any sense at all – good luck with that.
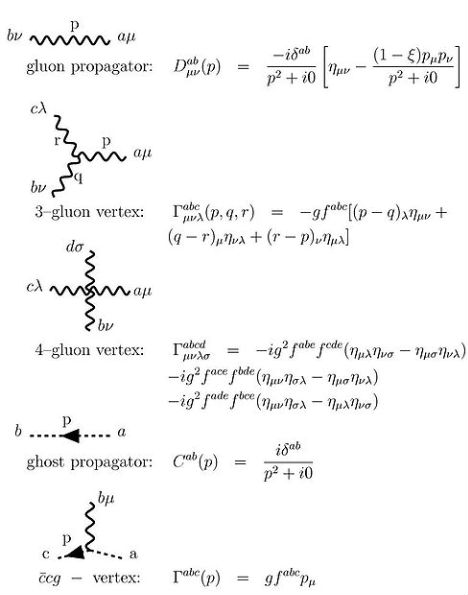
Yang-Mills Existence and Mass Gap
(image via: wikipedia)
The P Versus NP Problem isn’t the only unsolved mathematical problem currently drawing in lots of curious minds with a $1 million carrot. The Clay Mathematics Institute is also hoping that sum will lead to a solution to the Yang-Mills Existence and Mass Gap (and 6 other math problems as well). You’d have to prove that the quantum field theory underlying the Standard Model of particle physics (otherwise known as the Yang-Mills theory) is true, which is no easy task: it has to do with proving the existence of four-dimensional spacetime with solutions to the Yang-Mills equations as well as explaining a convoluted “mass gap”, which is the difference in energy between the vacuum and the next lowest energy state – are you lost yet?
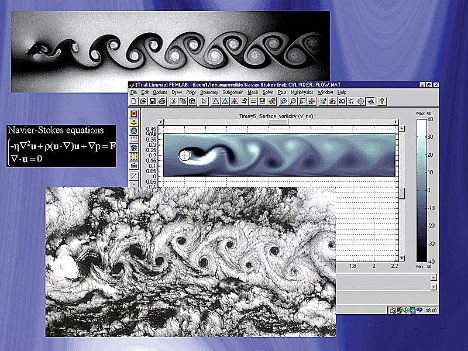
Navier-Stokes Existence and Smoothness Problem
(image via: climate audit)
How do you accurately describe the motion of a Newtonian fluid in space while taking into account variables like kinetic energy? Using a mathematical equation to discover solutions to this question may seem like an abstract concept, but a smooth solution in three-dimensional space and time would actually help solve real-world questions about the phenomenon of turbulence and could even help with global climate models in climate change research. If you want to claim yet another $1 million Millenium Prize from the Clay Mathematics Institute, you’ll need to either prove or disprove this statement: “In three space dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier–Stokes equations.” This problem is among the world’s least understood at a theoretical level, though it has been suggested that climate scientists are better suited to solving it than mathematicians, perhaps due to their more visually-oriented viewpoint.
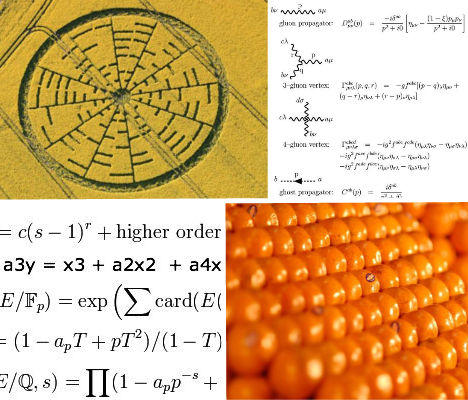
Euler’s Identity Crop Circle
(image via: the independent)
The ‘Euler’s Identity’ math problem may not be unsolved or particularly mysterious to mathematicians, but combine it with a crop circle, and you’re sure to puzzle the heck out of the general public. In May 2010, a bizarre 300-foot pattern of circles and lines appeared in a farmer’s field in the English countryside, and was later determined to be Euler’s Identity. The creators of this crop circle made a possibly intentional mistake, however: mathematician Dr. John Talbot at University College London notes “One of the discrepancies is that one part of the formula translates as ‘hi’ rather than ‘i,’ which could be somebody’s idea of a joke.”