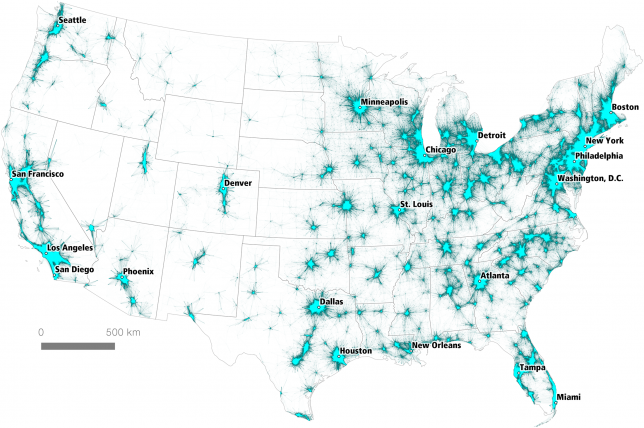
A new geographical study of the United States reveals the functional boundaries of megapolises around the country, defining them by usage rather than arbitrary political borders. Unlike gerrymandered districts or state lines, these sprawling areas are rooted in deep data analytics versus historical accident.
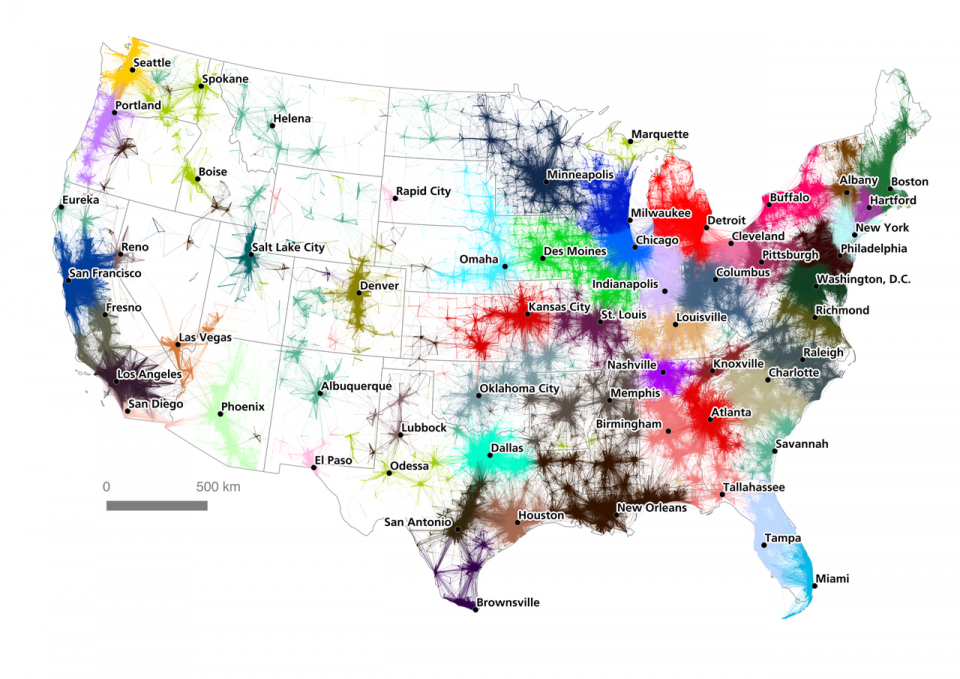
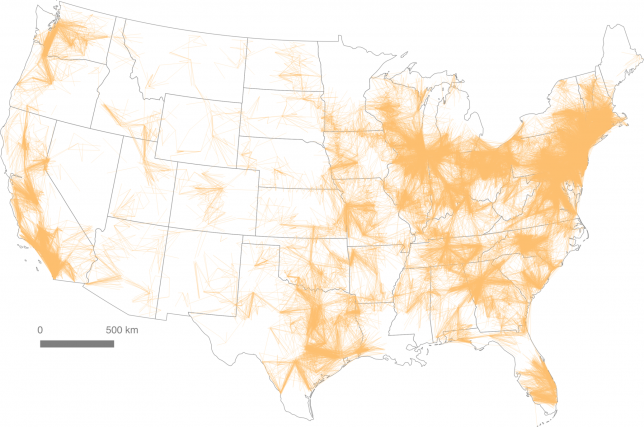
Historical geographer Garrett Dash Nelson teamed up with urban analyst Alasdair Rae to publish a paper using commuting information and computational algorithms. Studying over 4,000,000 commutes, they traced interconnections between economically connected points and reported the results in An Economic Geography of the United States: From Commutes to Megaregions.
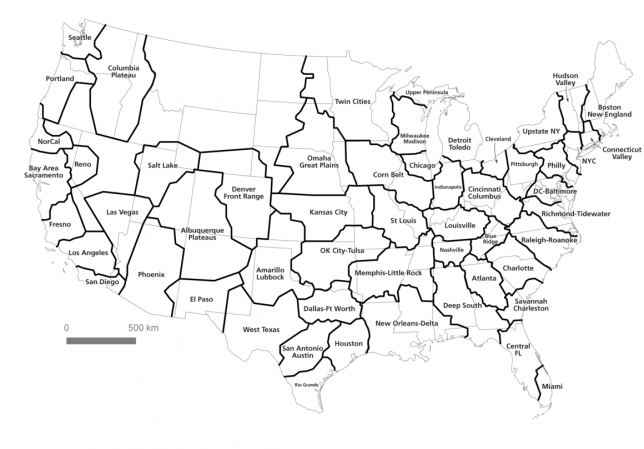
Taking it a step further, the authors also devised names for various megaregions extrapolated from the data – while semi-subjective, they start to give a sense of the real shape of metropolitan zones (and reveal areas where few residents and vast distances make it hard to define or confine regions).
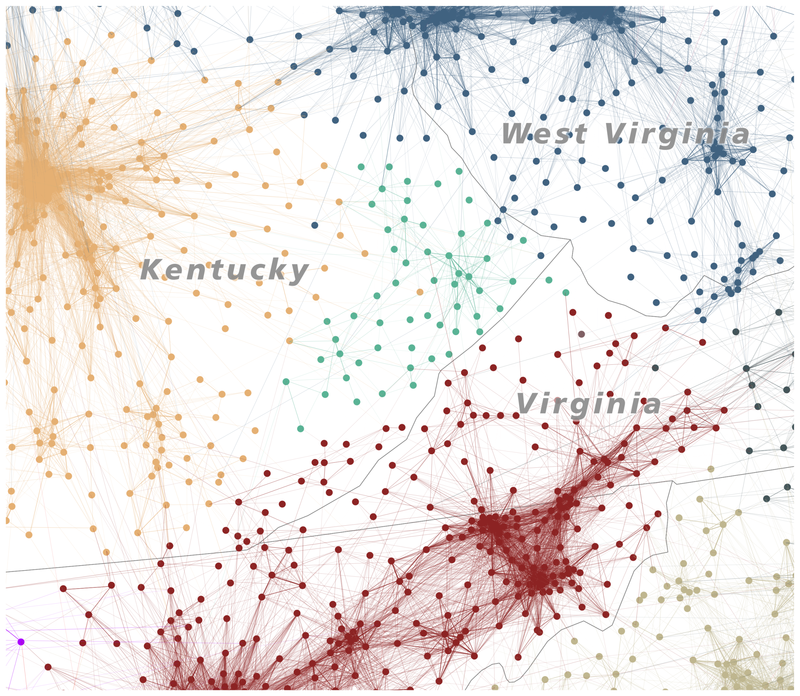
Some cities at the heart of various sub-regions are not surprising — San Francisco and Los Angeles were givens — but others may be new to some people, like Fresno, California. Many cities trace influence across state borders, like Minneapolis into Wisconsin or New York City into effectively every adjacent state. Some overlap while others are isolated, especially in the west.
In the end, this is not a definitive way to look at geography within the Lower 48, but it does start to push the observer to rethink conventional regions of influence and defined borders. From the abstract: “The emergence in the United States of large-scale ‘megaregions’ centered on major metropolitan areas is a phenomenon often taken for granted in both scholarly studies and popular accounts of contemporary economic geography. We compare a method which uses a visual heuristic for understanding areal aggregation to a method which uses a computational partitioning algorithm, and we reflect upon the strengths and limitations of both. We discuss how choices about input parameters and scale of analysis can lead to different results, and stress the importance of comparing computational results with ‘common sense’ interpretations of geographic coherence.”